目次
最初に二項分布の概要についてまとめます。
二項分布 \( \scriptsize B(n,p) \)
ある事象の結果が二択 であるような試行を n回おこなったとき、その事象が起こる回数 X に対する確率を示した分布
確率質量関数:
\( \scriptsize P( \tiny X=k \scriptsize )= \,_{n}C_{k} \, p^k (1-p)^{n-k} \)
期待値:\( \scriptsize E|X| = np \)
分散: \( \scriptsize V|X| = np(1-p) \)
グラフ(n=100 の例):
Excel関数: binomdist(X, n, p, 定数)
X:目的とする事象発生回数 (0〜nの整数)
n:試行回数
p:1回の試行で事象が発生する確率(0≦x≦1)
定数:0(false)…確率質量関数f(X)
1(true)…累積分布関数F(X)
二項分布は
ある事象の結果が二択 であるような試行を n回おこなったとき、その事象が起こる回数 X に対する確率を示した分布
です。
もうちょっとだけ具体的な例にします。
「コインを何回も投げた際に、表の出る回数に対してどのような確率になるか」コインをn回振って、表がk回出る確率Pはいくらでしょうか?という問題です。
コインを1回投げて表が出る確率は(イカサマでなければ)1/2ですが、一般化するためにあえて表の確率をp (0≦p≦1) として、表裏の確率が異なる場合について考えます。
1回目からk回目まですべて表が出る確率は \( \scriptsize p^k \) 、残り k+1 回目からn回目までが裏になる確率は\( \scriptsize (1-p)^{n-k} \) なので、1〜k回目が表で かつ k+1〜n回目が裏になる確率は \( \scriptsize p^k \cdot (1-p)^{n-k} \) となります。
しかし、k回表になるパターンは、n回のうちk回が表になる組み合わせの数(n個のなかからk個を選ぶパターン数) \( \scriptsize _{n}C_{k} \) 存在するので
表がk回出る確率Pは
\( \scriptsize P( k )= _{n}C_{k}\cdot p^k\cdot (1-p)^{n-k} \)
となります。
表が出る回数 k に対してその確率が右辺で決まるため、表が出る確率は確率変数であり、この式は確率分布を表したものだといえます。確率変数をXとして、X=kとなる場合のこの確率分布、これが二項分布です。
\( \scriptsize \color{red}{P( \tiny X=k \scriptsize )= \,_{n}C_{k} \, p^k (1-p)^{n-k} } \)
これを \( \scriptsize \color{red}{B(n,p) } \) と表します。
また、n, p のように、その値によって分布の形状が決まる(関数を特徴づける)数のことを母数といいます。
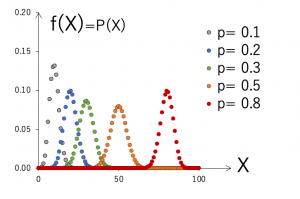
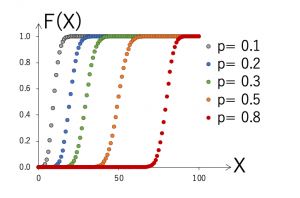
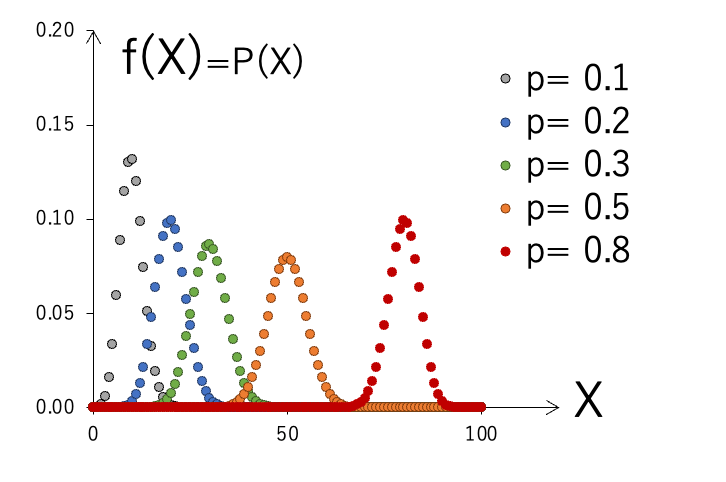
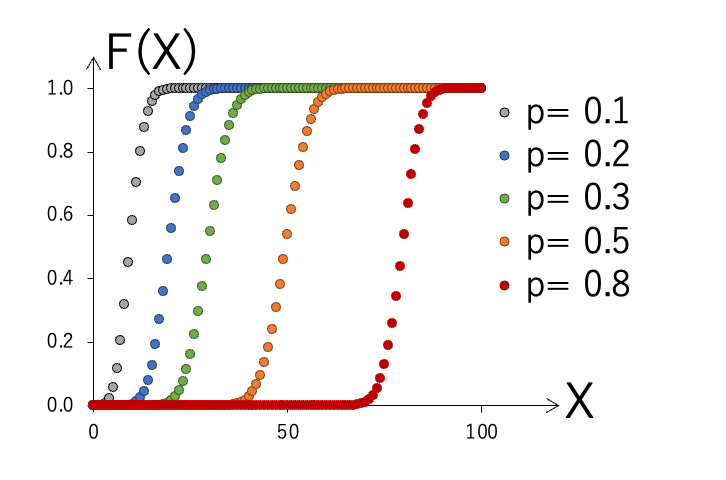
n=100(回)の場合の確率分布とその積算の分布を示します。1回の試行の確率pをいくつか変えて、グラフを比較してみます。
p=0.5の場合は、ちょうどX=50(回)のときに確率P(X)が最大となります。イカサマがないコインの表がでる確率はp=0.5ですが、100回コインを投げたとき、表が出る確率が一番多い回数は50回、と考えれば納得できます。
また、形状は左右対称で正規分布に似た釣り鐘型の分布をしています(実際に、nが十分大きい場合、二項分布は正規分布に近似することが示されるため、正規分布を用いて計算することもよく行われます)。
pが小さくなるとピークの位置は左に、pが1に近づくと右にシフトします。
1. 結果が二択になる試行であること
2. 繰り返しの各回の試行はそれぞれが独立であること(試行どうしが互いに影響を及ぼさないこと。1回目の試行によって2回目の確率が変わってはいけない)
3. 1回の試行においてある事象が発生する確率p は一定の値であること
二項分布の確率変数の期待値と分散について導出します(長いので結論だけ読んでもOK)。
二項分布の確率変数の期待値は
\( \scriptsize E|X| = \sum_{X=0}^{n} XP(X) = \sum_{k=0}^{n} kP( \tiny X=k \scriptsize ) \)
Σのなかはk=0のときゼロになるので
\( \scriptsize = \sum_{k=1}^{n} kP( \tiny X=k \scriptsize ) \)
\( \scriptsize = \sum_{k=1}^{n} k \, _{n}C_{k} p^k (1-p)^{n-k} \)
\( \scriptsize = \sum_{k=1}^{n} k \, \frac{n!}{(n-k)!k!} p^k (1-p)^{n-k} \)
kで約分して
\( \scriptsize = \sum_{k=1}^{n} \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
\( \scriptsize = \sum_{k=1}^{n} \frac{n\cdot (n-1)!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
npを前に出して
\( \scriptsize = np\sum_{k=1}^{n} \frac{(n-1)!}{(n-k)!(k-1)!} p^{k-1} (1-p)^{n-k} \)
\( \scriptsize = np\sum_{k=1}^{n} \frac{(n-1)!}{((n-1)-(k-1))!(k-1)!} p^{k-1} (1-p)^{n-k} \)
\( \scriptsize = np\sum_{k=1}^{n} \, _{n-1}C_{k-1} p^{k-1} (1-p)^{n-k} \)
k-1をk’に置き換えて
\( \scriptsize = np\sum_{k’=0}^{n-1} \, _{n-1}C_{k’} p^{k’} (1-p)^{(n-k’-1} \)
n-1をn’に置き換えて
\( \scriptsize = np\sum_{k’=0}^{n’} \, _{n’}C_{k’} p^{k’} (1-p)^{n’-k’} \)
二項定理より
\( \scriptsize = np\cdot \left\{ p+(1-p) \right\} ^{n’} \)
\( \scriptsize\color{red}{ = np} \)
二項分布の確率変数の分散は
\( \scriptsize V|X| = \sum_{X=0}^{n} (X-E|X|)^2 P(X) \)
\( \scriptsize = E|X^2| – (E|X|)^2 \)
ここで
\( \scriptsize E|X^2| = \sum_{k=0}^{n} k^2 P( \tiny X=k \scriptsize ) \)
\( \scriptsize = \sum_{k=0}^{n} k^2 \, _{n}C_{k} p^k (1-p)^{n-k} \)
\( \scriptsize = \sum_{k=0}^{n} k^2 \frac{n!}{(n-k)!k!} p^k (1-p)^{n-k} \)
Σのなかはk=0のときゼロになるので
\( \scriptsize = \sum_{k=1}^{n} k^2 \frac{n!}{(n-k)!k!} p^k (1-p)^{n-k} \)
k一個だけで約分
\( \scriptsize = \sum_{k=1}^{n} k \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
kの部分を(k-1)+1 に変形
\( \scriptsize = \sum_{k=1}^{n} \left\{ (k-1)+1 \right\} \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
二つの項に分ける
\( \scriptsize = \sum_{k=1}^{n} (k-1) \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
\( \scriptsize + \sum_{k=1}^{n} \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
第一項のΣのなかはk=1のときゼロになるので
\( \scriptsize = \sum_{k=2}^{n} (k-1) \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
\( \scriptsize + \sum_{k=1}^{n} \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
第一項を(k-1)で約分
\( \scriptsize = \sum_{k=2}^{n} \frac{n!}{(n-k)!(k-2)!} p^k (1-p)^{n-k} \)
\( \scriptsize + \sum_{k=1}^{n} \frac{n!}{(n-k)!(k-1)!} p^k (1-p)^{n-k} \)
第一項k-2をk’に、第二項k-1をk”に置き換える
\( \scriptsize = \sum_{k^\prime=0}^{n-2} \frac{n!}{(n-(k^\prime+2))!k^\prime!} p^{k^\prime+2} (1-p)^{n-(k^\prime+2)} \)
\( \scriptsize + \sum_{k”=0}^{n-1} \frac{n!}{(n-(k’+1))!k”!} p^{k”+1} (1-p)^{n-(k”+1)} \)
第一項はn(n-1)とp2、第二項はnとpを前に出す
\( \scriptsize = n(n-1) p^2 \sum_{k^\prime=0}^{n-2} \frac{(n-2)!}{(n-(k^\prime +2))!k^\prime!} p^{k^\prime} (1-p)^{(n-k^\prime)-2} \)
\( \scriptsize + np \sum_{k”=0}^{n-1} \frac{(n-1)!}{(n-(k”+1))!k”!} p^{k”} (1-p)^{(n-k”)-1} \)
二項定理より
\( \scriptsize = n(n-1)p^2 \left\{ p+(1-p) \right\}^{n-2} \)
\( \scriptsize + np \left\{ p+(1-p) \right\}^{n-1} \)
\( \scriptsize = n(n-1)p^2 + np \)
よって
\( \scriptsize V|X| = E|X^2| – (E|X|)^2 \)
\( \scriptsize = n(n-1)p^2 + np -(np)^2 \)
\( \scriptsize = n^2p^2-np^2 + np -n^2p^2 \)
\( \scriptsize \color{red}{= np(1-p)} \)
となります。(長かった。。。)
