目次
変数のなかで、「ある値をとる」確率が存在する変数のことを確率変数といいます。
たとえば
さいころを投げて出る目は{1, 2, 3, 4, 5, 6}のいずれかの値をとり、それぞれの目が出る確率は1/6 である(決まった確率が存在する)ことから、さいころを投げて出る目は確率変数であるといえます。
確率変数の値(=さいころの出る目) を X とおくと
Xの目が出る確率は
\( \scriptsize P(X)= \small \frac{1}{6} \quad \tiny (X=1,2,3,4,5,6) \)
また、「さいころを投げて3の目が出る事象の確率は 1/6 である」 ことは
\( \scriptsize P(3)= \small \frac{1}{6} \) または \( \scriptsize P( \tiny X=3 \scriptsize )= \small \frac{1}{6} \)
のように表されます。
なお、一般的に確率変数は「X」のように大文字で表記されます。
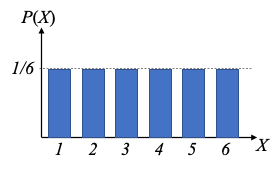
「確率変数の値」と「確率変数がその値をとる確率」との関係性を示したものを確率分布といいます。
例えば、さいころを投げる場合、
1から6までの確率変数の値に それぞれ 1/6 という確率が対応しているため、
値が1/6で一定の「確率分布」です。
最初にサイコロを例にして確率変数について触れましたが、実は確率変数は大きく二つに分けられます。
確率変数のなかで、変数がとびとびの値をとる変数のことを離散型確率変数といいます。
例としては、サイコロの目の数字、トランプの札の数字、コインの裏表(裏=0、表=1などとした場合) などが挙げられます。
一方、変数が連続した値をとる確率変数を連続型確率変数といいます。
身長、重量、温度 などがこれにあたります。
確率変数と同様に、確率分布も大きく二つに分類されます。
確率変数が離散型である場合の確率分布を離散型確率分布といいます。また、離散型確率変数Xがある値xをとる確率を関数 f(x) として表したものを確率質量関数といいます。
\(\scriptsize f(x)=P( \tiny X=x \scriptsize ) \)
確率質量関数のグラフは、下のように不連続な点からなるグラフになり、縦軸f(xi)の値が確率P(xi)を示します。
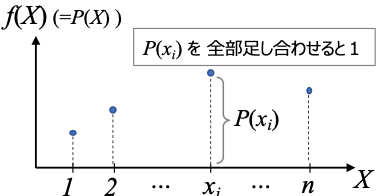
全事象が起こる確率は、各確率変数における確率を全個数n個足し合わせたものであり、その値は1になります。
\(\scriptsize \sum_ {i=1}^n P( x_i )=1 \)
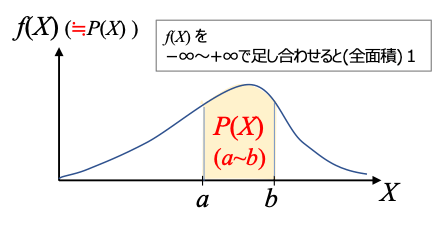
一方、確率変数が連続型である場合の確率分布を連続型確率分布といいます。また、連続型確率変数Xがある値xをとるときの「確率密度」を関数 f(x) として表したものを確率密度関数といいます。
※注意しなくてはいけないのは、縦軸のf(x)は確率密度であって、確率ではないということです。連続型の場合、ある確率変数X=xでは確率は意味を持ちません。(どういうこと???)
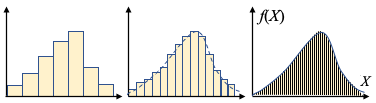
かなり乱暴な説明かもしれないですが、ヒストグラムをイメージすると…
データのサイズが非常に大きな場合のヒストグラムについて、階級(区間)を狭くしていくと、極限では連続型の関数のグラフになります。階級が狭くなるにつれて、各微小区間に含まれる度数はどんどん小さくなります。
しかし、もしそのままのスケールで短冊だけを細くしたら、(あたりまえですが)グラフ上の縦軸の値(短冊の高さ)は変わらないですよね。この場合、極限にスライスした細い短冊の高さ、すなわち、あるX=xにおけるf(x)は、データの存在量ではなく、「存在しやすさ・現れやすさ」(ちょっとあいまいな言い方ですが…)を示し、これに短冊の横幅dxをかけあわせた(正確には、「ある区間積分した」)面積が存在量を表すことになります。
別の言い方をすれば、幅を持たない短冊(言い換えると、Xがある一つの値であるとき)は面積がないので、存在量を示すことはできないことになります。
上のはなしが確率分布における確率密度f(x)と確率P(x)に対応しているといえます。確率密度は、確率変数がとりうる値の「現れやすさ」を示します。
よって、f(x)をある区間a〜bで積分することではじめて確率F(x)(a〜b)になります。
くりかえしになりますが、X=xとなる (ある値xをとる) 確率はゼロになり
\(\scriptsize P( \tiny X=x \scriptsize )=0 \)
a≦X≦b となる確率は、その範囲の確率密度の積分となり
\(\scriptsize P( \tiny a≦X≦b \scriptsize )=\int_b^a f(x)dx \)
全確率は1になります。
\(\scriptsize \int_{-\infty} ^{\infty} f(x)dx =1 \)
サイコロのはなし(離散型変数の例)に戻ります。
サイコロを振ったときに出てくる目の数の平均値は
\( \scriptsize 1\times\frac{1}{6} + 2\times\frac{1}{6} + 3\times\frac{1}{6} + \cdots + 6\times\frac{1}{6} = 3.5\)
このように、ある試行を行ったときに結果として得られる数値の平均値のことを期待値といいます。
サイコロの例からわかるように、離散型変数の場合、期待値は確率変数X=xi と 確率P(X=xi)の積 を足し合わせたものになります。
したがって離散型の確率変数の期待値は次の式のようになります。
\( \scriptsize E|X|=\sum_{i=1}^n (x_i \cdot p_i ) \)
ただし、確率変数 \(\scriptsize X=x_i \) 確率 \(\scriptsize P(X=x_i)=p_i \)
離散型の確率変数の分散は、期待値からの差(偏差)の二乗値 と 確率の積 を足し合わせたものになります。
\(\scriptsize V|X|= \sum_{i=1}^n (x_i −E|X|)^2 p_i \)
一方、連続型変数の場合は足し合わせが積分になります。
離散型では、期待値を求めるときには\( \scriptsize x_i \cdot p_i \) を足し合わせましたが、この確率 \( \scriptsize p_i \) は連続関数の場合は\( \scriptsize f(x) dx \) に相当します(微小の横幅dx をかけて面積にすることで確率になるため)。
よって、\( \scriptsize p_i \)をこの\( \scriptsize f(x) dx \) に置き換えて足し合わせ→連続関数では積分すればよいわけです。
連続型の確率変数の期待値は
\( \scriptsize E|X|=\int_{-\infty}^{\infty} x f(x) dx \)
分散も同様に、確率 \( \scriptsize p_i \)を\( \scriptsize f(x) dx \) に置き換え、足し合わせを積分に置き換えると、
連続型の確率変数の分散は
\(\scriptsize V|X|= \int_{-\infty}^{\infty} (x−E|X|)^2 f(x) dx \)
これまでの内容をまとめますと次のようになります。
| 離散型 | 連続型 | |
| 確率変数 | 離散型確率変数 | 連続型確率変数 |
| 特徴 | 値がとびとび | 値が連続(隙間ない) |
| 例 | サイコロの数字など | 重量、温度など |
| 確率分布 | 離散型確率分布 | 連続型確率分布 |
| 分布を表す関数f(x) | 確率質量関数 | 確率密度関数 |
| 確率P(X)との関係 | \(\tiny P(X=x)=f(x) \) | \(\tiny P(a≦X≦b)=\int_b^a f(x)dx \) |
 |  | |
| 期待値 | \( \tiny E|X|=\sum_{i=1}^n (x_i \cdot p_i ) \) | \( \tiny E|X|=\int_{-\infty}^{\infty} x f(x) dx \) |
| 分散 | \(\tiny V|X|= \sum_{i=1}^n (x_i −E|X|)^2 p_i \) | \(\tiny V|X|= \int_{-\infty}^{\infty} (x−E|X|)^2 f(x) dx \) |
