目次
ポアソン分布について、最初に概要を示します。
ポアソン分布 \( \scriptsize Po(\lambda) \)
ある期間に平均λ回しか起こらない事象について、その事象が起こる回数 X に対する確率を示した分布
確率質量関数:\( \scriptsize P( \tiny X=k \scriptsize ) = \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
期待値:\( \scriptsize E|X| = \lambda \)
分散: \( \scriptsize V|X| = \lambda \)
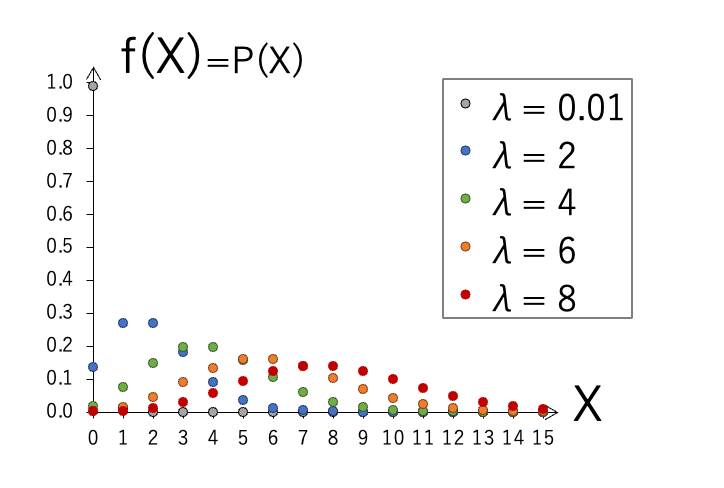
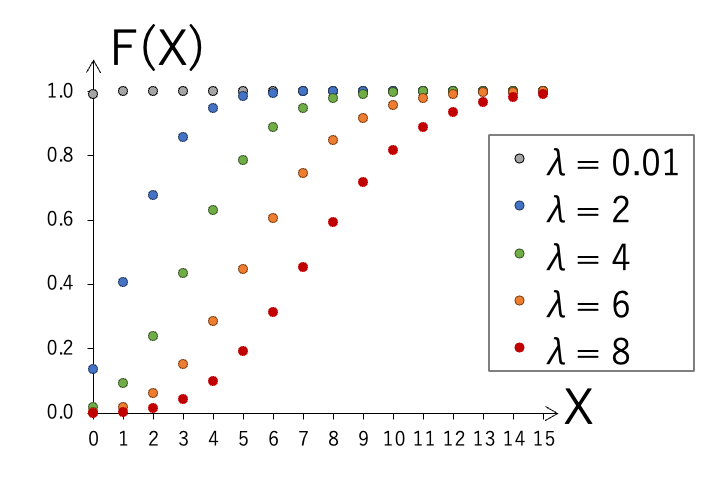
グラフ:
Excel関数: poisson(X, λ, 定数)
X:目的とする事象発生回数
λ:事象が発生する平均回数
(期間内の回数や単位人数あたりの数)
定数:0(false)…確率質量関数f(X)
1(true)…累積分布関数F(X)
ポアソン分布とは
まれにしか起こらない事象について、その事象が起こる回数 X に対する確率を示した分布
です。「ある期間(範囲)において平均 λ 回しか起きないようなまれな事象が、その期間(範囲)においてX回起きる確率」がわかります。
少し具体的な例にします。1,000個に1個の割合で不良品が発生する(確率p=0.001)製品について、10個抜き取りをして検査したときに不良品がk個含まれる(X=k)確率を考えます。
二項分布を適用すると
\( \scriptsize P( \tiny X=k \scriptsize ) = \, _nC_k \, p^k(1-p)^{n-k} \)
\( \scriptsize = \, _{10}C_k \cdot 0.001^k (1-0.001)^{10-k} \)
となります。
そして、確率変数Xの期待値は
\( \scriptsize E(X)=np= 10 \times 0.001 = 0.01 \)
となり、これは故障発生の平均個数を示します(故障をみつける ”平均回数” といえます)。このようにnが十分大きく、pが非常に小さい値の場合、np を一定の値 λ とすると、確率変数はポアソン分布に従います。
ある期間に平均λ回起こる現象がその期間にk回起こる確率、すなわち確率変数X=kとなる確率P(X)は
\( \scriptsize P( \tiny X=k \scriptsize ) = \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
となります。これがポアソン分布の確率関数です。
ポアソン分布のグラフを示します。
λが0.01と小さな値の場合、X=0のときに最も確率が高く、X=1になると急激に確率が減り、Xがそれ以上大きい範囲では確率はほぼゼロになります。右側に広い裾野をもつ分布です。
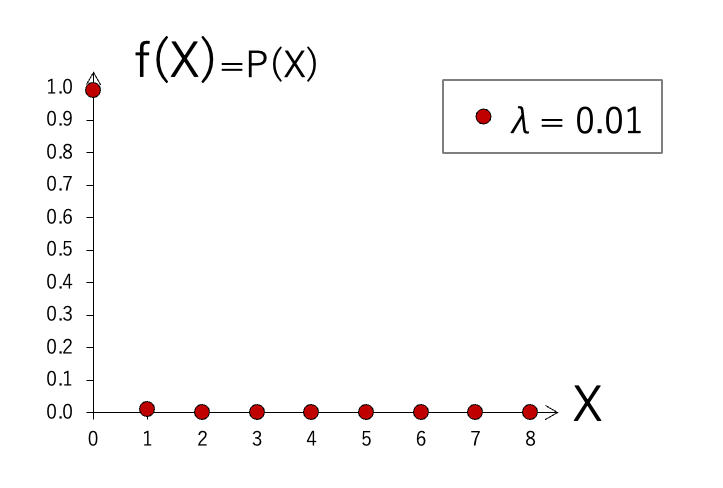
平均回数λの値を変化させて、グラフの形状を比較してみます。


λが大きくなるにつれて、ピークが右側にシフトし、形状が左右対称に近づき、正規分布に似た形状に変化していきます。
ポアソン分布における確率変数の期待値は
\( \scriptsize E|X| = \sum_{X=0}^{n} XP(X) = \sum_{k=0}^{n} kP( \tiny X=k \scriptsize ) \)
\( \scriptsize = \sum_{k=0}^{n} k \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
\( \scriptsize = \sum_{k=0}^{n} k \small \frac{\lambda ^k}{(k-1)!} \scriptsize e^{-\lambda} \)
\( \scriptsize = \lambda \sum_{k=0}^{n} k \small \frac{\lambda ^{k-1}}{(k-1)!} \scriptsize e^{-\lambda} \)
\( \scriptsize \color{red}{ = \lambda } \)
となります。
ポアソン分布における確率変数の分散は
\( \scriptsize V|X| = \sum_{X=0}^{n} (X-E|X|)^2 P(X) \)
\( \scriptsize = E|X^2| – (E|X|)^2 \)
ここで
\( \scriptsize E|X^2| =\sum_{k=0}^{n} k^2 \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
\( \scriptsize =\sum_{k=0}^{n} (k(k-1)+1) \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
\( \scriptsize =\sum_{k=0}^{n} k(k-1) \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} +\sum_{k=0}^{n} k \small \frac{\lambda ^k}{k!} \scriptsize e^{-\lambda} \)
第二項はλなので
\( \scriptsize =\sum_{k=0}^{n} \small \frac{\lambda ^k}{(k-2)!} \scriptsize e^{-\lambda} +\lambda \)
\( \scriptsize =\lambda ^2 \sum_{k=0}^{n} \small \frac{\lambda ^{k-2}}{(k-2)!} \scriptsize e^{-\lambda} +\lambda \)
\( \scriptsize = \lambda ^2 + \lambda \)
よって
\( \scriptsize V|X| = E|X^2| – (E|X|)^2 \)
\( \scriptsize V|X| = ( \lambda ^2 + \lambda ) – \lambda ^2 \)
\( \scriptsize \color{red}{ = \lambda } \)
となります。
