目次
エントロピーのまとめにおいて、熱力学第二法則としてエントロピー増大則を示しました。熱力学第二法則は、いろいろな研究者によって、切り口を変えてさまざまな表現によって示されています。
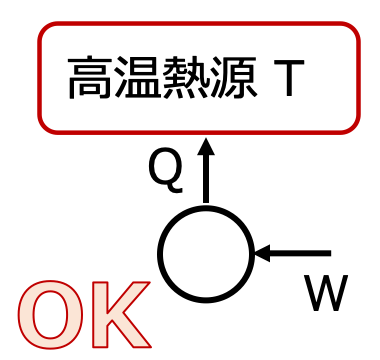
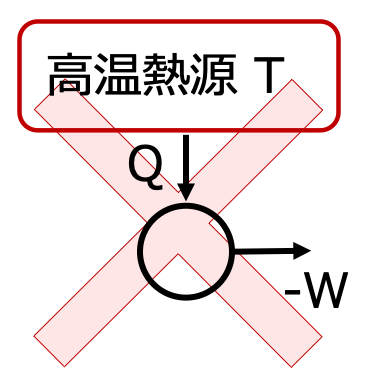
トムソンの法則
仕事を全て熱に変えることはできても 熱を全て仕事に変えることはできない
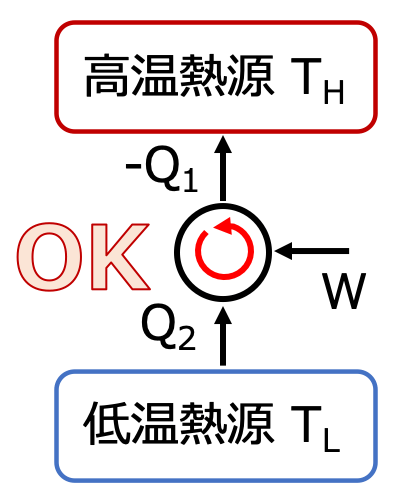
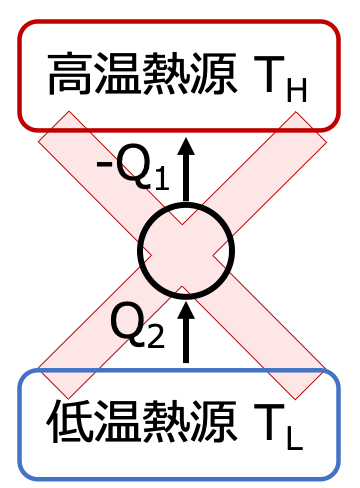
クラウジウスの法則
何の影響もなく 低温の物体から 高温の物体へ 熱を移すことはできない
※クラウジウスの法則はトムソンの法則と同じ
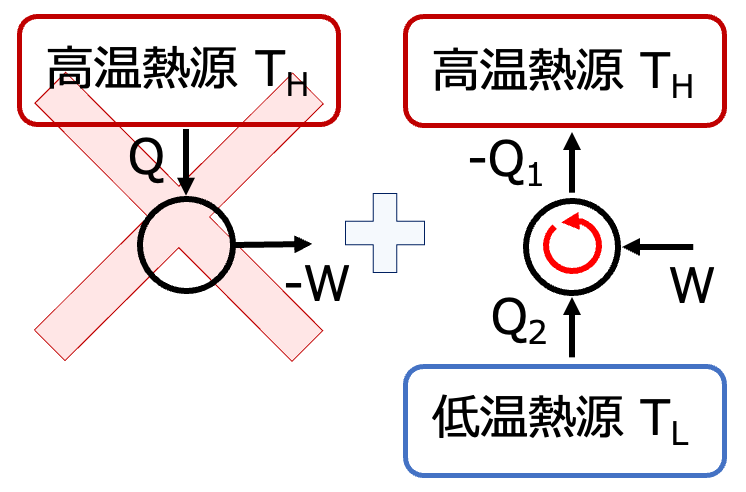
トムソンのNGのサイクルと
逆カルノーサイクルを
組み合わせる
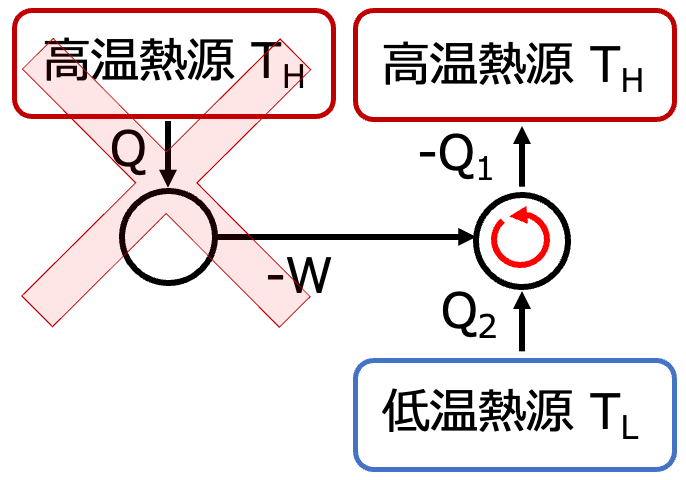
これを一つのサイクルとみることができるので・・・
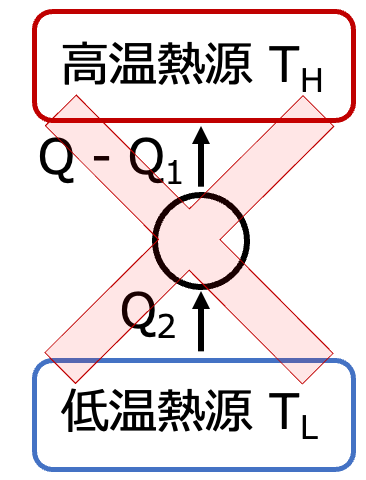
クラウジウスの法則の
NGのサイクルと等しいことがわかる
オストワルドの原理
第二種永久機関(熱を受け取って永久に動き続けるサイクル)は実現不可能である
系が高温熱源から熱を受け取ると高温熱源はわずかに温度が下がり、低温熱源へ放出するとは低温熱源はわずかに温度が上がります。そして、最終的には高温熱源と低温熱源の温度が等しくなるため、サイクルが回らなくなってしまいます。
この機関が永久に動くためには低温熱源から高温熱源へ熱を戻す必要がありますが、これはトムソンの法則にて実現不可能なので、第二種永久機関も不可能なわけです。
カルノーの定理 から
\( \scriptsize \eta ‘ = \frac{Q_1 + Q_2}{Q_1} \leq \frac{T_H – T_L}{T_H} \)
となり、これを変形すると
\( \scriptsize \frac{Q_1}{T_H} + \frac{Q_2}{T_L} \leq 0 \)
となります。この等号が成立するのは熱サイクルが可逆の場合です。
熱源を低温熱源・高温熱源の二つから数を増やしていき、n個の熱源からなるサイクルの場合は次の式が成り立ちます。
クラウジウスの不等式
\( \small \Sigma \frac{Q_i}{T_i} \scriptsize \leq 0 \)
Qi は熱源から系に入る熱(系が吸熱する場合 Qi >0、放熱する場合 Qi <0)
Ti は熱源の温度
※等号は可逆サイクルの場合に成立
系が熱源から微小の熱を受けとりまた放出して熱サイクルが回っていく場合を考えると、クラウジウスの不等式の左辺は
\( \small \Sigma \frac{\Delta Q_i}{T_i} \)
温度が連続的に変化していくサイクルの場合は、ΔQi を極限0と考え
\( \small \Sigma \frac{\Delta Q_i}{T_i} \) → \( \small \color{red}{\int \frac{\delta Q}{T} } \)
とあらわすことができます。さらに準静的過程の場合は系と熱源では熱的平衡を保ちつつサイクルが回るため、系と外界(熱源)の温度は等しい、つまり T = 系の温度 とみなすことができます。
さて、この準静的サイクル上に、A,Bの2点を置き、サイクルをA→B(熱をQとする)とB→A(熱をQ’とする)の二つに分けると
\( \small \int^{B}_{A} \frac{\delta Q}{T} + \int^{A}_{B} \frac{\delta Q’}{T} \scriptsize =0 \)
※準静的過程なのでクラウジウスの式は等号になる
準静的な過程なのでサイクルを逆回転させることができるため、B→Aの経路を反転させると
\( \small \int^{B}_{A} \frac{\delta Q}{T} + \int^{B}_{A} \frac{-\delta Q’}{T} \scriptsize =0 \)
∴\( \small \int^{B}_{A} \frac{\delta Q}{T} = \int^{B}_{A} \frac{\delta Q’}{T} \scriptsize \)
つまり \( \small \int^{B}_{A} \frac{\delta Q}{T} \) という式の値は、始点Aと終点Bが同じであれば経路によらず一定であることを示しています。
そこで、状態量としてエントロピーSを導入し、
\( \scriptsize \Delta S_{A→B} = S_B – S_A = \small \int^{B}_{A} \frac{\delta Q}{T} \)
が成立すると定義します。
ここまで準静的過程で考えてきましたが、今度は、準静的ではない過程を含む場合を考えます。準静的ではない(≒不可逆)過程の場合はクラウジウスの式は不等号になるので
\( \small \int^{B}_{A} \frac{\delta Q}{T} + \int^{A}_{B} \frac{\delta Q’}{T} \scriptsize \leq 0 \)
左辺の第二項が準静的過程、第一項が非準静的過程とすると
\( \small \int^{B}_{A} \frac{\delta Q}{T} \leq \int^{B}_{A} \frac{\delta Q’}{T} \scriptsize = \Delta S_{A→B} \)
となり、一般化するとエントロピー変化ΔSについて
\( \small \color{red}{\Delta S \geq \int \frac{\delta Q}{T} } \) (等号は可逆の場合)
さらに、断熱系の場合はδQ=0となるので
\( \small \color{red}{\Delta S \geq 0 } \) (等号は可逆の場合)
とエントロピー増大則が導かれます。
