昔から苦手だった熱力学。復習してはすぐに忘れていくので、備忘録にまとめました。
目次
熱力学第一法則に入る前に、基本的な用語の復習から。
物理化学では系および外界という言葉を常に使用します。
「系」とは「考察の対象として着目するまとまり」のことをいいます。ケミカルの分野では、たとえば、反応をおこなうフラスコなどの中身の状態 などが系に該当します。
「外界」は、境界を隔てた「外側の空間」のことをいいます。上の例では、フラスコなどの反応容器が境界で、外側の実験室の空間が外界 ということができます。
系と外界は、境界を介して 熱・仕事・物質 のやりとりをおこなうことで、体積・圧力などの変化 や 反応 等が進みます。
これらのやりとりの種類によって、系は大きく以下に分類されます。
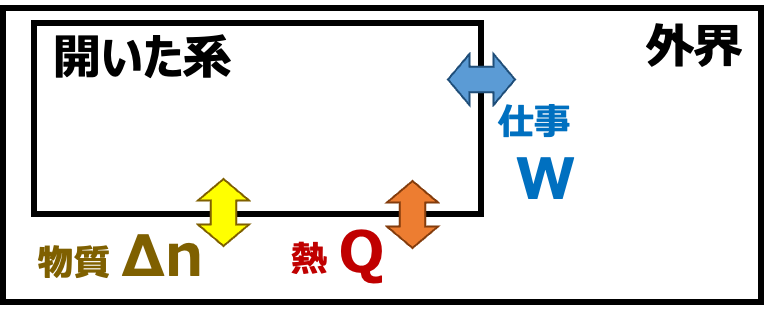
①開いた系 外界とのあいだで熱・仕事・物質のやりとりがある系
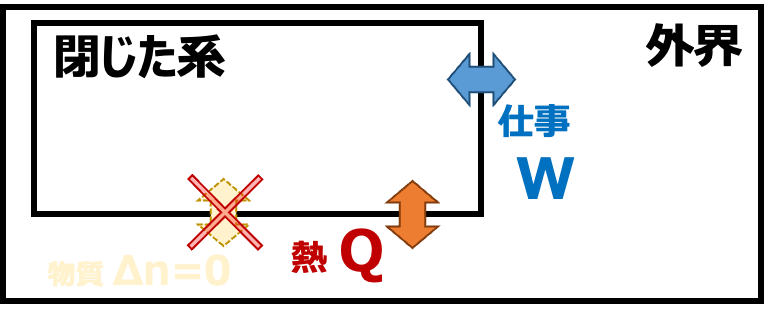
②閉じた系 外界と熱・仕事のやりとりはおこなうが、物質のやりとりができない系
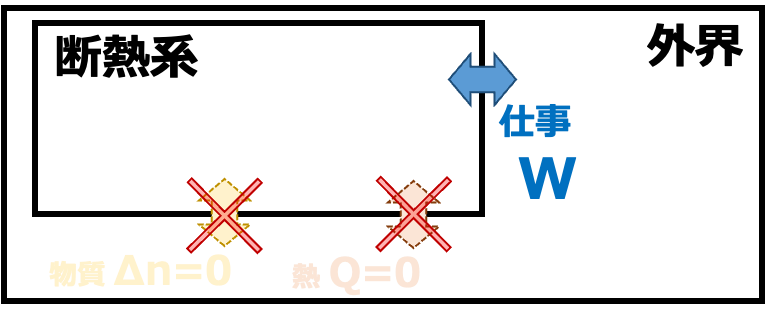
③断熱系 外界と仕事のやりとりはおこなうが、熱・物質のやりとりができない系
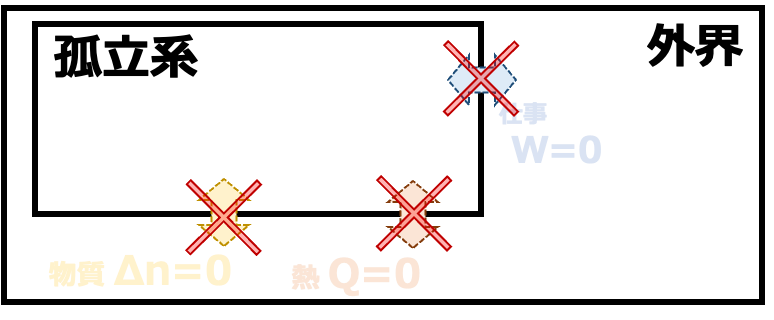
④孤立系 外界とのあいだで熱・仕事・物質のやりとりができない系
状態量とは、平衡状態のときにその状態のみで決まる量のことをいいます。状態量の変化量は最初と最後の状態によって決まり、その過程の経路によりません。
状態量の例: 温度、圧力、内部エネルギー、エントロピー など
状態量でないもの:熱、仕事 など
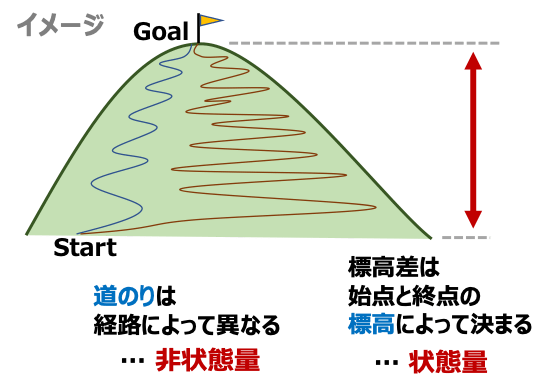
状態量は、性質によって示強性の量と示量性の量に分けられます。
示強性の量:物質の量に無関係な状態量。温度、圧力 など
示量性の量:物質の量に比例する状態量。体積、質量、内部エネルギーなど
熱力学の第一法則は「エネルギー保存則」とも呼ばれます。エネルギーは、何もないところから発生しないし、突如消えてしまうこともない、ということです。
少し学問らしく数式を使うと
\( \small \Delta U = Q + W \)
「系の内部エネルギーの増加 ΔU は 系に入る熱 Q と 系になされる仕事 W の和に等しい」ことを示しています。
第一法則は微分形で次のようにも表されます。
\( \small dU = \delta Q + \delta W \)
状態量でないものにはdではなくδをつけて区別します
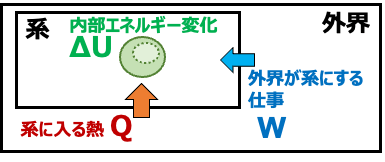
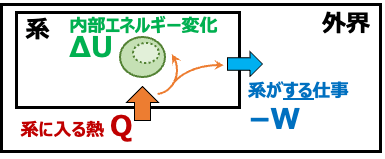
別の表現を使うと
「系に熱量Qを与えると、内部エネルギーの増加分ΔU と 系が外界に対してする仕事 −W に振り分けられる」ともいえます。
\( \small Q = \Delta U +( – W) \)
熱も仕事もエネルギーですが、各エネルギーについてもう少し詳しくみますと
ΔU:系の変化にともなう内部エネルギー変化(☞ 内部エネルギー)
内部エネルギーUは状態量なので、
ΔUは途中の経路には依存しません。
Q :変化の過程で 系が外界から吸収した熱量
(経路に依存するため状態量ではない)
W :変化の過程で 系が外界から「受ける」仕事
(経路に依存するため状態量ではない)
(W>0、−W<0のとき 系に対して仕事がされる)
−W:変化の過程で 系が外界に対して「する」仕事
(経路に依存するため状態量ではない)
(W<0、−W>0のとき 外界に向けて仕事をする)
このとき注意が必要なのは、熱Qおよび仕事Wの符号は、系に対して入ってくる方向を正とします。なので、系が外界に対して仕事をする場合、その仕事は(符号が逆の)「−W」となり、「−W」が正になります。
ややこしいことに、この「系がする仕事 −W」を「W」として表記する教科書もあるので、常に系が仕事を「するのか」「されるのか」を意識する必要があります。
この「系がする仕事」は、力学的な仕事のほか、電気的な仕事などいろいろな形態があり、これら仕事の合計量になります。しかし、熱力学において着目する仕事は、熱から変換された力学的エネルギーの部分になるので、「系がする仕事=力学的仕事」として考えていきます。
化石燃料や原子炉などによって得られる熱から力学的エネルギーへの変換(たとえば、ピストン運動に変えて車のエンジンを動かす、タービンを回して発電をすることによりさらに電気エネルギーへ変換する、など)によって私たち生活が支えられているように、与えられた熱量からどれだけ仕事としてのエネルギーを取り出せるか、ということは非常に重要であるとわかります。
実際の系について考えていきます。
熱力学での力学的仕事は、一般に 気体の体積変化によるものになります。
そこでまず、この「気体の体積変化による仕事」についてその中身をみていきます。毎度おなじみのピストンの図です。
内部の気体が膨張するとき、ピストンは、外界から一定の気圧pを受けながら(押し広げようとして)移動します。これが、気体の体積変化による仕事(系が外界に対してする仕事)になります。
高校物理で出てきた「仕事=力 ✕ 距離」です。
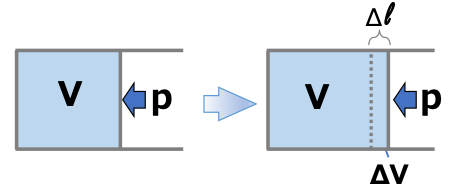
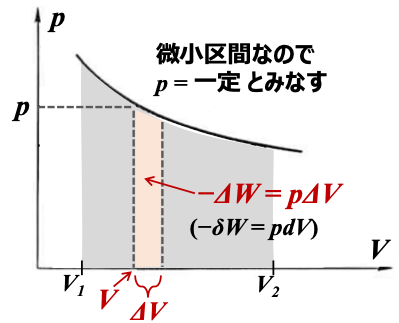
ピストンの壁の面積をAとすると、壁にかかる力は \( \scriptsize F=A \times p \)
壁が 微小な距離 \( \scriptsize \Delta l \) だけ動いたとすると、系が外界に対してした仕事は
\( \scriptsize \color{red}{-\Delta W} \color{}{= F\Delta l = (A \times p)\Delta l } \color{red}{= p \Delta V} \)
となります。
※この圧力は系の圧力ではなく、外界の圧力であることに注意(外からの気圧に対抗してピストンを動かそうとする仕事なので)。
微分形で書くと
\(\scriptsize -\delta W = pdV \)
となり、pが変化する過程ではこれを積分することで仕事が求められます。
\(\scriptsize \color{red}{ – W = \int^{V_2}_{V_1} pdV } \)
気体が膨張するか または 収縮するか によって、仕事の符号が変わります。
系が体積膨張して外界に仕事をする → \( \scriptsize \Delta V>0\,⇒\, W<0 \, (-W>0) \)
系が外界から仕事をされて体積収縮する → \( \scriptsize \Delta V<0\,⇒\, W>0 \, (-W<0) \)
n mol の理想気体が一定温度Tにおいて体積V1からV2に等温可逆的に変化(正確には 準静的変化:熱の平衡状態を常に保ちながら変化)した場合を考えます。
(※系と外界の温度がTで一定でありながらも、系と外界のあいだで熱を授受しています。ただし、温度勾配による熱の流れは考えません)
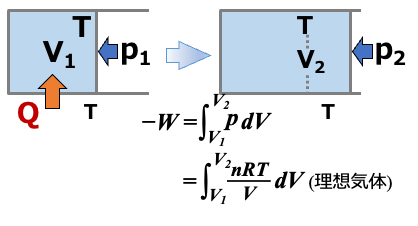
系には 外界に仕事をした分だけ 熱的平衡を保ちながら外界から熱が補給され、常に温度はTで一定になっています( \( \scriptsize \color{red}{\Delta T=0} \))。
一定温度では、ジュールの法則により内部エネルギーは体積によらず一定(☞自由膨張の項を参照)なので
\( \scriptsize \Delta U = Q + W = 0 \)
∴ \(\scriptsize \color{red}{Q = -W} \)
外界に仕事をした分だけ外界から熱が補給されることを示しています。
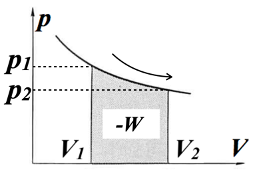
状態(p1, V1)から(p2, V2)への過程において系が外界に対してする仕事は、理想気体の場合には状態方程式 \(\scriptsize pV=nRT \) をもちいることにより
\(\scriptsize \color{red}{- W }\color{}{=\int^{V_2}_{V_1}pdV = \int^{V_2}_{V_1}\frac{nRT}{V} dV = nRT[\ln{V}]^{V_2}_{V_1} } \)
\(\scriptsize \color{red}{= nRT\ln\frac{V_2}{V_1}= nRT\ln\frac{p_1}{p_2}} \)
となって、Q、Wを求めることができます(このときのグラフのp-V曲線は、理想気体の状態方程式の関係を示したものになります)。
ちなみに、「あれ?pは外界の気圧だったはずだけど、系の内部の気体の状態方程式を使っていいの?」という疑問が出るかもしれないですが、これは、この等温変化が準静的過程を経る前提にしているため、系と外界のあいだで常に熱的平衡が保たれており、外界の圧力=系の圧力 としてよいからです。つまり、外界の気圧に対する体積変化の仕事の式に、系の状態方程式の圧力を使用してもよいということになります(準静的過程でない場合はこのような置き換えはできません)。
外界の圧力が一定の条件下における可逆変化を考えます。
化学分野などでは一般的な系になります。例えば、開放された反応容器内の反応によって内部の気体が体積変化するような場合が該当します。

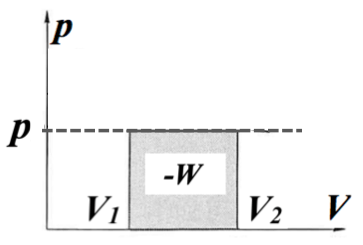
系が外界にする仕事は
\( \scriptsize \color{red}{ -W} \color{}{ = \int^{V_2}_{V_1} pdV = p \int^{V_2}_{V_1} dV } \color{red}{= p(V_2 -V_1) } \) (pは一定であるため)
内部エネルギーの変化は
\( \scriptsize \Delta U = Q +W =Q-p(V_2 -V_1) \)
ですが、定積熱容量 \( \scriptsize C_V = \left( \frac{\partial U}{\partial T} \right)_V \) から
\( \scriptsize\color{red}{ \Delta U} = \int_{T_1}^{T_2} C_V dT \color{red}{= C_V(T_2-T_1)} \)
となり、ΔUを求めることができます。
※注意:定圧での変化ですが、内部エネルギーを求めるときには定圧熱容量ではなく定積熱容量を使います。
体積一定 \( \scriptsize \Delta V =0 \) の条件下における変化を考えます。
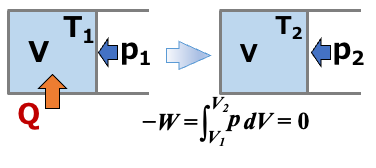
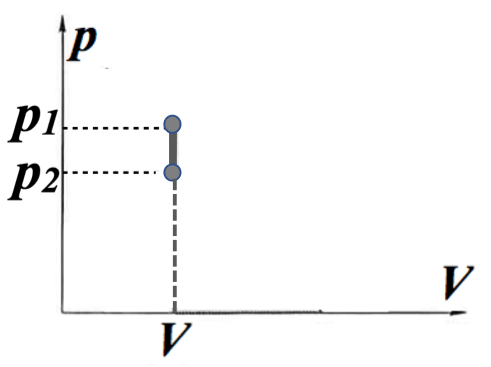
系が外界にする仕事は、体積変化がないためゼロになります。
\( \scriptsize \color{red}{ -W} \color{}{ = \int^{V}_{V} p dV = p\cdot 0} \color{red} {=0} \)
内部エネルギーの変化は
\( \scriptsize \color{red}{ \Delta U} \color{}{ = Q + W} \color{red}{ = Q} \)
系に加えられた熱は、すべて内部エネルギーの増加に使われます。
また、定積熱容量 \( \scriptsize C_V = \left( \frac{\partial U}{\partial T} \right)_V \) から
\( \scriptsize\color{red}{ \Delta U} = \int_{T_1}^{T_2} C_V dT \color{red}{= C_V(T_2-T_1)} \)
となり、ΔU、Qを求めることができます。
断熱により、系と外界のあいだの熱の出入りが無い系における体積変化について考えます。
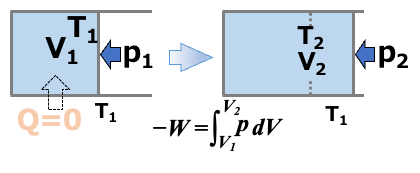
断熱であるため、系と外界の熱のやりとりはなく、
\( \scriptsize \color{red}{Q=0} \)
\( \scriptsize \color{red}{\Delta U} \color{}{ = Q + W} \color{red}{ = W} \color{}{ = -\int^{V_2}_{V_1} pdV } \)
体積変化にともなう仕事によって、内部エネルギーが変化します。
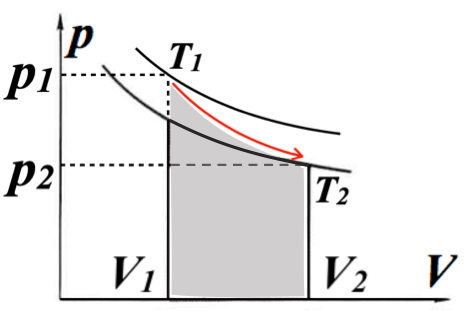
断熱膨張: ΔV>0であるため ΔU <0 すなわち ΔT <0 温度が低下する
断熱圧縮: ΔV<0であるため ΔU >0 すなわち ΔT >0 温度が上昇する
また、理想気体であったとしても、状態1(p1, V1)と状態2(p2, V2)は異なるp-V曲線上にあるため、等温変化のように理想気体の状態方程式をそのまま用いて求めることはできませんが、定積熱容量 \( \scriptsize C_V = \left( \frac{\partial U}{\partial T} \right)_V \) より求めることができます。
\( \scriptsize \color{red}{W} \color{}{ = \Delta U = \int^{T_2}_{T_1} C_V dT} \color{red}{ =C_V(T_2-T_1)} \)
また、理想気体が断熱変化を行う場合は、その気体の圧力p と体積V の間には
ポアソンの関係式 \( \scriptsize PV^{\gamma}= \)一定 \( \scriptsize TV^{\gamma -1}= \)一定 \( \scriptsize \gamma= \left( \frac{C_p}{C_V} \right) \)
が成り立ちます。
ジュールの実験という実際におこなわれた実験についてみていきます。
気体の入ったフラスコと真空状態のフラスコをコックをはさんでつないだもの(この内部が系になります)を断熱材のなかにいれて温度一定の平衡状態になるまで置きます。平衡になったら、コックを一気に開き、気体の温度変化を確認します。この結果、コックを開く前後での温度変化はありませんでした。
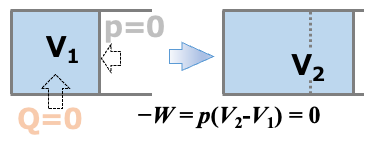
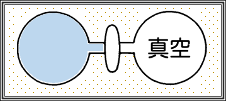
まず、外界から系への熱の移動はなかったので
\( \scriptsize \color{red}{Q=0}\)
となります。
真空への気体の膨張は、ピストンに対して外界からの圧力がかかっていない \( \scriptsize p=0 \) の状態での体積変化なので、系が外界に対してする仕事は
\( \scriptsize \color{red}{ -W} \color{}{=\int^{V_2}_{V_1} p dV = p \int^{V_2}_{V_1} dV = 0\cdot (V_2 – V_1) } \color{red}{=0} \)
となり、仕事をしていないことになります。この部分が、断熱変化とは大きく異なる点です。
よって、内部エネルギー変化は
\( \scriptsize \color{red}{\Delta U} \color{}{= Q+W} \color{red}{ =0}\)
となります。
また、内部エネルギーの変化は、全微分によって
\( \scriptsize dU= \left( \frac{\partial U}{\partial T} \right)_{V} dT + \left( \frac{\partial U}{\partial V} \right)_{T} dV \quad (=0) \)
と表されますが、実験の結果からdT=0なので
\( \scriptsize \left( \frac{\partial U}{\partial V} \right)_T dV=0 \)
かつ dV≠0 なので
\( \scriptsize \color{red}{\left( \frac{\partial U}{\partial V} \right)_T =0} \)
が導き出され、温度一定の場合は内部エネルギーは体積変化の影響を受けないことが示されます。
系と外界とのやりとり による 系の分類
| 開いた系 | Q≠0 W≠0 Δn≠0 |
| 閉じた系 | Q≠0 W≠0 Δn=0 |
| 断熱系 | Q=0 W≠0 Δn=0 |
| 孤立系 | Q=0 W=0 Δn=0 |
熱力学第一法則
\( \small \Delta U = Q + W \) \( \small Q = \Delta U + (-W) \)
ΔU:内部エネルギーの変化 Q:系に入る熱 W:系がされる仕事
Uは状態量、Q, Wは非状態量
5種類の変化
| 等温変化 | \(\scriptsize \Delta U=0 \) \(\scriptsize Q=-W=nRT \ln \frac{V_2}{V_1}=nRT \ln \frac{P_1}{P_2} \) |
| 等圧変化 | \(\scriptsize \Delta U=Q+W=C_V (T_2 – T_1) \) \(\scriptsize -W=p(V_2 – V_1) \) |
| 等積変化 | \(\scriptsize \Delta U=Q=C_V (T_2 – T_1) \) \(\scriptsize -W=0 \) |
| 断熱変化 | \(\scriptsize \Delta U=W=C_V (T_2 – T_1) \) \(\scriptsize Q=0 \) |
| 自由膨張 | \(\scriptsize \Delta U=Q=W=0 \) |
