目次
カルノーサイクルとは、フランスの物理学者カルノーによって考え出された、熱を仕事へ効率よく変換するために考えられた理想的な機関(エンジン)のことです。理想的機関なので実際には存在しないですが、熱から仕事への理論上の変換効率を知ることができます。
エンジンのシリンダ(=系になります)は、外部の高温熱源(T=TH)からQ1(>0)の熱をうけとって、低温熱源(T=TH)へQ2(<0)の熱を排出する過程において、系が仕事Wをします。入ってきた熱の一部を捨てながら仕事を行うため、その熱量の差が仕事となります。
式で表すと \( \scriptsize -W = Q_1-(-Q_2) = Q_1+Q_2 \) となります。
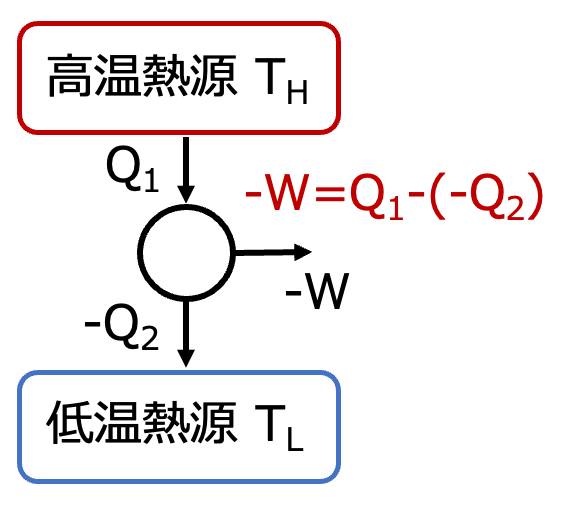
ここで、系に入ってきた熱に対してどれだけ仕事に変換できたかを示す指標として
熱効率 \(\scriptsize\color{red}{\eta =\frac{-W}{Q_1} = \frac{Q_1 +Q_2}{Q_1} = \frac{T_H-T_L}{T_H}} \)
と定義します。
熱効率は、二つの熱源の温度TH, TLによって決まります。(理由はのちほど示します。)
低温熱源への放熱を小さくすることで熱効率が向上します。
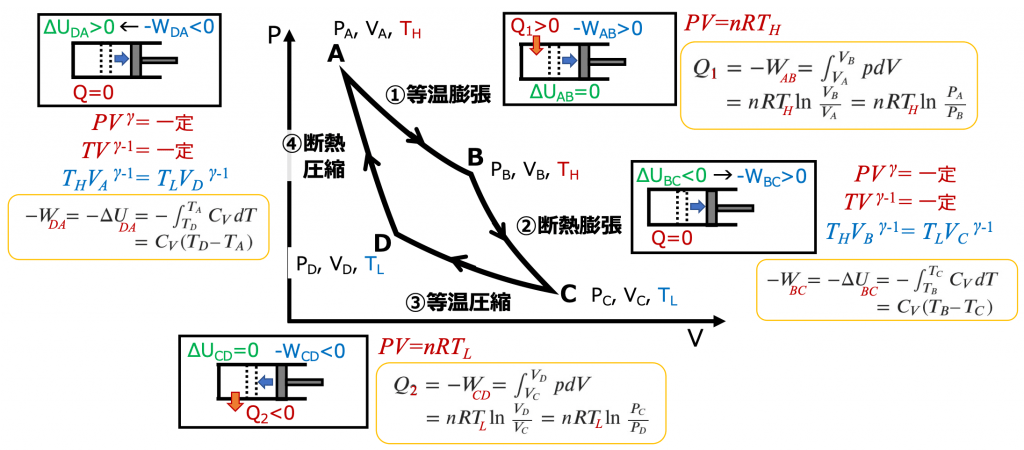
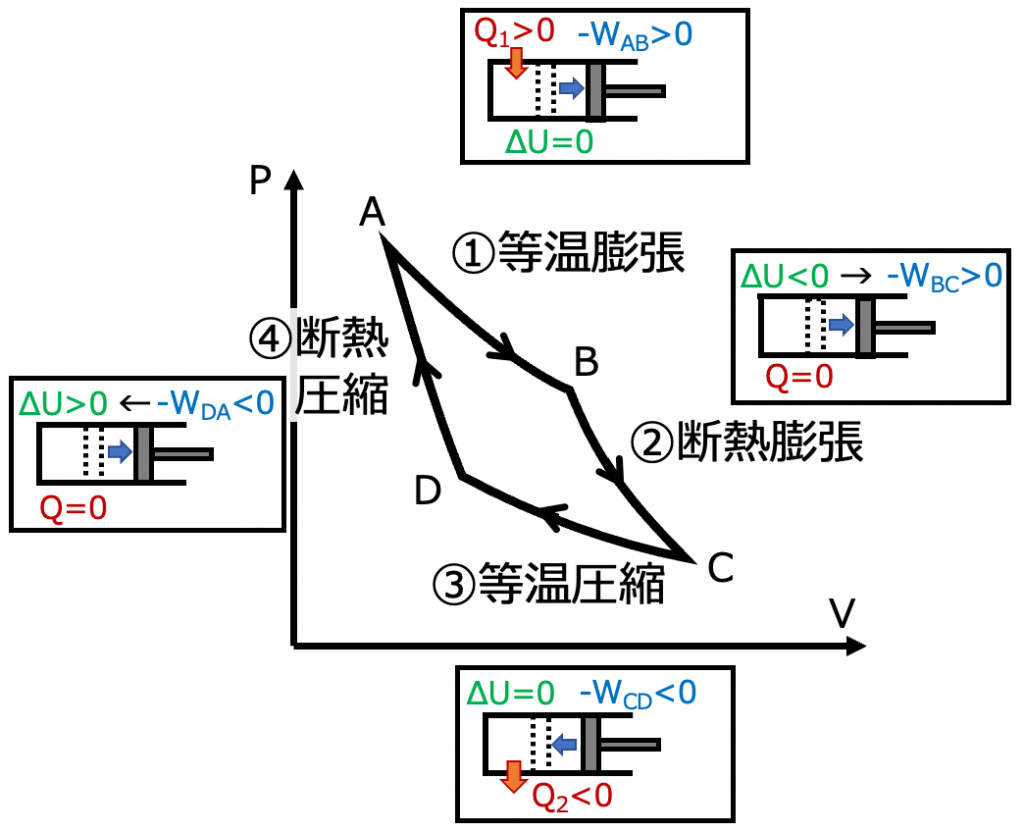
カルノーサイクルは、理想気体が 等温膨張、断熱膨張、等温圧縮、断熱圧縮 の四つの段階を経て元にもどる可逆循環過程(準静的過程のサイクル)です。
可逆(準静的)過程ですので、系に仕事を与えることによってサイクルを逆に回し、低温熱源から高温熱源へ熱を移動させることも可能で、これを逆カルノーサイクルといいます(原理的にはヒートポンプがこれにあたります)。
順方向のサイクルについて、各過程をみていきます。
①等温膨張(A→B)
体積膨張によっての温度が下がろうとする分、外界から熱が注入されるため、温度一定で平衡を保ったままです。等温過程なので内部エネルギーは一定です(ΔU=0)。
\(\scriptsize Q_1= -W_{AB} = \int^{V_B}_{V_A} p dV = \int^{V_B}_{V_A} \frac {nRT_H}{V} dV \)
\(\scriptsize = nRT_H \ln \frac{V_B}{V_A} = nRT_H \ln \frac{P_A}{P_B} \)
Q1 > 0 なので \(\scriptsize V_A<V_B\) 体積膨張し、\(\scriptsize P_A>P_B\) 圧力は低下します。
②断熱膨張(B→C)
系は外界から完全に断熱されている状態(Q=0)で、Q=ΔU-WよりΔU= W。内部気体は膨張することで外界へ仕事をします(-W>0)。
\(\scriptsize -W_{BC} = -\Delta U_{BC} = -\int^{T_C}_{T_B} C_V dT = C_V(T_B – T_C) \, \tiny (= C_V(T_H – T_L) ) \)
-WBC > 0 なので \(\scriptsize T_B > T_C \) となって温度は低下します。
③等温圧縮(C→D)
等温過程なのでΔU=0。
\(\scriptsize Q_2= -W_{CD} = \int^{V_D}_{V_C} p dV = \int^{V_D}_{V_C} \frac {nRT_L}{V} dV \)
\(\scriptsize = nRT_L \ln \frac{V_D}{V_C} = nRT_L \ln \frac{P_C}{P_D} \)
Q2 < 0 なので \(\scriptsize V_C>V_D\) 体積減少し、\(\scriptsize P_C<P_D\) 圧力は増加します。
④断熱圧縮(D→A)
断熱なのでQ=0。Q=ΔU-WよりΔU= W。内部気体は圧縮されることで外界から仕事をうけます(-W<0)。
\(\scriptsize -W_{DA} = -\Delta U = -\int^{T_A}_{T_D} C_V dT = C_V(T_D – T_A) \, \tiny (= C_V(T_L – T_H) ) \)
-WDA < 0 なので \(\scriptsize T_A > T_D \) となって温度は増加します。
カルノーサイクルのする仕事
1サイクル回る間にシリンダ内部の気体(系)がする仕事について考えます。これは、①〜④の各過程の仕事の合計になるので
\(\scriptsize -W = nRT_H \ln \frac{V_B}{V_A} + C_V(T_H – T_L) + nRT_L \ln \frac{V_D}{V_C} + C_V(T_L – T_H) \)
\(\scriptsize = nRT_H \ln \frac{V_B}{V_A} + nRT_L \ln \frac{V_D}{V_C} \)
ところで、②④の断熱過程では、それぞれ
\( \scriptsize T_H V_B^{\gamma-1}=T_L V_C^{\gamma-1} \) \( \scriptsize T_H V_A^{\gamma-1}=T_L V_D^{\gamma-1} \)
が成り立ちます。この二式を割ると
\( \scriptsize \frac{T_H V_B^{γ-1}}{T_H V_A^{γ-1}}=\frac{T_L V_C^{γ-1}}{T_L V_D^{γ-1}} \)
\( \scriptsize \left( \frac{V_B}{V_A} \right)^{γ-1}=\left( \frac{V_C}{V_D} \right)^{γ-1} \)
∴\( \scriptsize \frac{V_B}{V_A}=\frac{V_C}{V_D} \)
よって、仕事の計算のはなしに戻って、この式を代入すると
\(\scriptsize -W = nRT_H \ln \frac{V_B}{V_A} + nRT_L \ln \frac{V_D}{V_C} \)
\(\scriptsize = nRT_H \ln \frac{V_B}{V_A} + nRT_L \ln \frac{V_A}{V_B} \)
\(\scriptsize = nR(T_H-T_L) \ln \frac{V_B}{V_A} \)
カルノーサイクルの系が受けとる熱量
1サイクル回る間にシリンダ内部の気体(系)がうけとる熱量の収支計は、①〜④の各過程の熱の入りの合計になるので(※等温圧縮過程は熱が出て行くので負になりますが)
\(\scriptsize Q = nRT_H \ln \frac{V_B}{V_A} +0+ nRT_L \ln \frac{V_D}{V_C} +0 \)
\(\scriptsize = nRT_H \ln \frac{V_B}{V_A} + nRT_L \ln \frac{V_A}{V_B} = nR(T_H-T_L) \ln \frac{V_B}{V_A} \)
カルノーサイクルの熱と仕事
上で求めた熱量と仕事量を比較するとわかるように、カルノーサイクルの熱の出入りの差は、系がした仕事に等しくなります(Q1−(−Q2) = −W)。つまり、系への熱の出入りの差分が仕事に変換されたことがわかります。
最初に述べたように、投入した熱量Q1に対してどれだけ仕事に変換できたかについては、熱効率として表されます。
熱効率 \(\scriptsize \eta =\frac{-W}{Q_1} = \frac{Q_1 +Q_2}{Q_1} = \frac{nR(T_H-T_L) \ln \frac{V_B}{V_A}}{nRT_H \ln \frac{V_B}{V_A} } \)
\(\scriptsize = \frac{T_H-T_L}{T_H} \)
よって、熱効率は高温熱源と低温熱源の温度で決まることがわかります。
なお、この効率は理想的な状態での値であり。現実世界ではシリンダの摩擦などによってエネルギーが消費されるため、これよりも低い値になります。つまり、カルノーサイクルで求められる効率は、系から取り出すことのできる仕事量の理論的最大値に基づいた効率(理論上最大の効率)です。

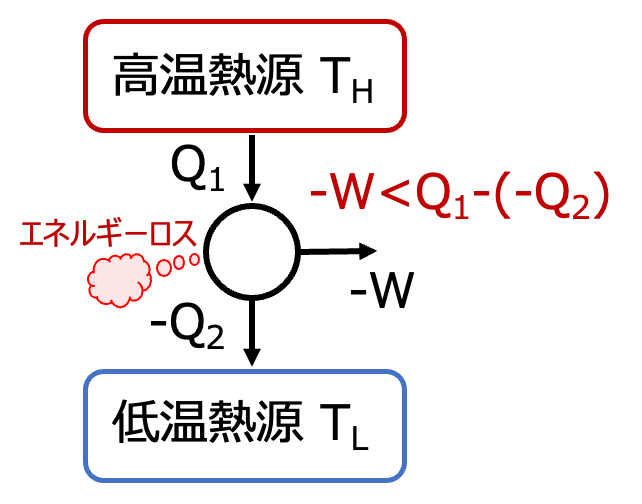
「不可逆な機関の熱効率 \(\scriptsize \eta ‘ \) は、可逆機関 \(\scriptsize \eta \)の熱効率を超えることはなく、可逆機関の熱効率は二つの熱源の温度によって決まる」
\(\scriptsize \color{red}{\eta ‘ \leq \eta} \)
\(\scriptsize \color{red}{\eta = \frac{T_H-T_L}{T_H} } \)
カルノーサイクル
二つの熱源を利用して、熱を仕事へ効率よく変換するために考えられた理想的な機関
等温膨張、断熱膨張、等温圧縮、断熱圧縮 の四つの段階を経て元にもどる可逆循環過程(準静的過程のサイクル)
高温熱源(T=TH)からQ1(>0)の熱をうけとって、低温熱源(T=TH)へQ2(<0)の熱を排出する過程において、系が仕事Wをします。

熱効率 \(\scriptsize \eta =\frac{-W}{Q_1} = \frac{Q_1 +Q_2}{Q_1} = \frac{T_H-T_L}{T_H} \)
カルノーの定理
不可逆機関の熱効率 \(\scriptsize \eta ‘ \leq \) 可逆機関の熱効率 \(\scriptsize \eta \)
熱効率は高温熱源と低温熱源の温度によって決まる。
\(\scriptsize \eta = \frac{T_H-T_L}{T_H} \)
