エンタルピーにつづき、エントロピーです。
名前は似てますが全く異なるものです。
目次
エンタルピーによって、定圧変化における系の熱の出入り(発熱量、吸熱量)を示しました。しかし、この変化自体が進行するかどうかについてはまだよくわかりません。自発的に変化が進行する方向(反応式の右向きあるいは左向きに進むか)を示す指標が欲しいところです。
そこでエントロピー S という状態量を導入し、その変化量を次のように定義します。
\( \scriptsize \color{red}{d S= \frac{\delta Q}{T}} \) 積分系で\( \scriptsize \color{red}{\Delta S= \int\frac{\delta Q}{T}} \)
ここで、Qは準静的(≒ 可逆的)に系に入ってきた熱量になります。
つまり、準静的変化でない(≒ 非平衡状態)の場合は上の等式は成立しないので、非平衡状態を含めて一般化した式にすると
\( \scriptsize \color{red}{d S \geq \frac{\delta Q_{irr}}{T_外}} \) 積分系で\( \scriptsize \color{red}{\Delta S\geq \int\frac{\delta Q_{irr}}{T_外}} \)
となります。(☞クラウジウスの不等式)
これを、さらに断熱過程の場合においていいかえると、熱の出入りがない(δQ=0)ことから
熱力学第二法則 (エントロピー増大則)
断熱過程(δQ=0)において \( \scriptsize \color{red}{\Delta S \geq 0} \)
※等号は理想的な可逆変化(準静的過程) の場合だけ成り立つ。
※自然に起こる変化(自発的変化) は不可逆変化(準静的過程でない) だから、等号は成立せずΔS>0となる。
ここで重要なことは、法則が成立するのは断熱系の場合なので、「系と外界との間での熱のやりとりはない」ことが必要です。しかし、系と外界の間で「仕事のやりとりがあっても成立」しますので、混同しないように注意が必要です。
☞断熱系と孤立系の違いは…「系と外界」を参照
実際にいくつかの系についてエントロピーがどのようになるのかを見ていきます。
理想気体について、状態1(P1, V1, T1)→状態2(P2, V2, T2)の等温膨張(準静的過程)を考えます(T2 = T1)。
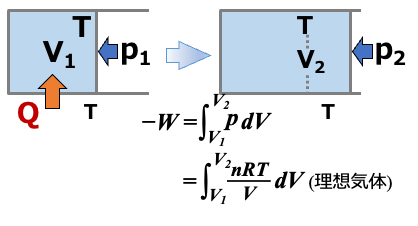
系がする仕事 −W は
\(\scriptsize -W=\int^{V_2}_{V_1}pdV =\int^{V_2}_{V_1} \frac{nRT}{V}dV \)
(∵準静的過程なので外界と系の圧力は同じ 。系の圧力を使って状態方程式を適用)
\(\scriptsize=nRT_1 \ln\frac{V_2}{V_1} \) (∵準静的過程なのでTは一定(T1)で推移→積分記号の外側に出して)
熱力学第一法則より
\(\scriptsize Q=\Delta U – W \)
\(\scriptsize = 0 – W \) (∵ 等温ΔT=0 なので ΔU=0)
\(\scriptsize = nRT_1 \ln\frac{V_2}{V_1} \)
よって、系のエントロピー変化は
\(\scriptsize \Delta S = \int \frac{dQ}{T} = \frac{Q}{T_1} = nR \ln \frac{V_2}{V_1} \)
となります(∵準静的過程なので等号が成立 \(\scriptsize \Delta S = \int \frac{dQ}{T} \))。
ここで疑問が発生します。上で求めた系のエントロピー変化は体積が膨張すれば正になりますが、熱力学第二法則より「準静的過程なのだからエントロピー変化ΔSはゼロではないのか?(ΔS≧0 の等号成立の場合ではないか?)」という疑問です。
しかし、法則が成立する条件「断熱過程において」を見落としています。上で考えている系は等温膨張過程なのでそもそもエントロピー増大則の条件を満たしていないわけです。
…ん?ではそもそも、断熱過程以外の変化ではエントロピーを考えてはいけないのか? そんな使えない物を何故わざわざ導入しなくてはいけなかったのか? 体積膨張ではなく体積収縮する場合はΔSは負になってエントロピーは減少するけどいいの?(等温収縮はできないってこと?)???
(学部生時代はこのあたりで教授の説明がよくわからなくなり、化学熱力学の授業をドロップアウトしていったような記憶があります。。。)
このように、断熱系(または孤立系)でない系については、外界のエントロピー変化を考え、系と外界を含めた一つの「孤立系」として考えます(「系+外界」(=孤立系) と その外側の「外外界 (そんな言葉はないですが) 」とのあいだでは熱のやりとりはないものと考えます)。
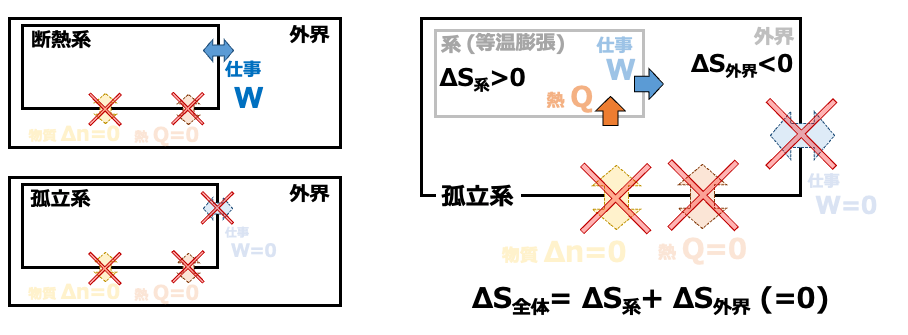
外界のエントロピー変化について考えていきます。系がδQの熱を受け取る分、外界はδQを失います。よって、
\( \scriptsize \Delta S_{外界} = \int\frac{-\delta Q}{T} \) (∵外界は十分に大きいので熱的平衡状態とみなされ、等号が成立)
\( \scriptsize = -\frac{Q}{T_1} = -nR \ln \frac{V_2}{V_1} \)
となります。
そして、外界と系を一つにまとめた孤立系のなかでのエントロピー変化は
\( \scriptsize \Delta S_{全体} = \Delta S_{系}+\Delta S_{外界} \)
\( \scriptsize = nR \ln \frac{V_2}{V_1} +(-nR \ln \frac{V_2}{V_1} )=0 \)
となり、準静的過程であることと矛盾しないことがわかります。この変化は可逆的に進行することが可能なわけです。
理想気体について、状態1(P1, V1, T1)→状態2(P2, V2, T2)の断熱自由膨張を考えます(自由膨張なのでT1=T2)。
「考えます」と言っておきながらですが、自由膨張は準静的な過程ではない(∵系と外界との圧力平衡を保ちながら推移していないから)ので、エントロピー変化を直接求めることができないのではないか(∵\(\tiny \Delta S = \scriptsize \int \frac{dQ}{T} \) の等号が成立しないから)という疑問がわきます。
たしかに非平衡の変化ではエントロピー変化を直接求めることは困難ですが、エントロピーが状態量であることを利用して求めることができます。
つまり、非平衡過程の自由膨張の代わりに、計算で求めることができる別の過程を使って考えます。たとえば準静過程である等温膨張変化で考えれば、仕事WからQを求めてΔSにたどり着くことができます。始点と終点が同じであれば、どのルートをたどって求めようとも、ΔSは同じだからです。
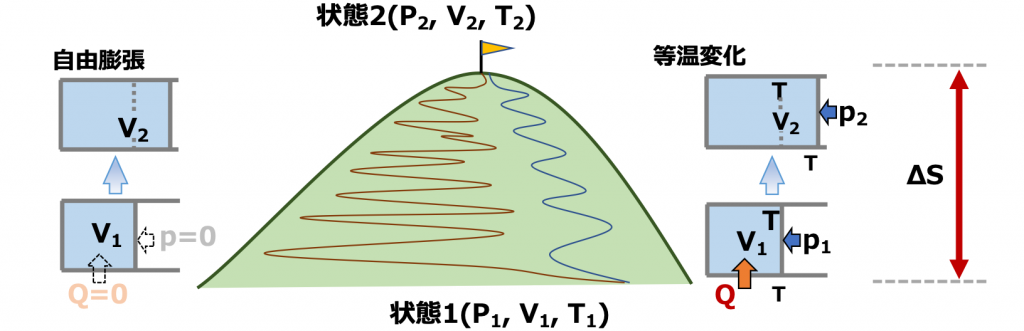
等温(準静的)過程の場合は、前の項でまとめたように、
\(\scriptsize -W=nRT_1 \ln\frac{V_2}{V_1} \)
\(\scriptsize Q=\Delta U – W = nRT_1 \ln\frac{V_2}{V_1} \)
∴\(\scriptsize \Delta S = \int \frac{dQ}{T} = \frac{Q}{T_1} = nR \ln \frac{V_2}{V_1} \)
となり、体積が膨張する(V2>V1)ことから ΔS>0 となって、変化が自発的に進行することが示されます。
このように、エントロピー変化を求める際に、「エントロピーは状態量である」ことが効果を発揮します。
自由膨張は系自体が外界と熱のやりとりのない断熱系なので、変化の自発性については系のエンタルピーだけ考えればよいはずですが、念のため外界のエンタルピー変化はどうなっているか考えてみます。
外界のエントロピー変化は系のエントロピー変化の逆符号であり、
また外界は十分に大きいため外界のなかでは常に熱的に平衡状態とみなせ、
さらに、断熱のため \(\scriptsize \delta Q= 0 \) だから
\(\scriptsize \Delta S_外= -\int \frac{\delta Q}{T_外} =0 \)
全体としては
\(\scriptsize \Delta S_{全体} = \Delta S_{系} + \Delta S_{外} = nR \ln \frac{V_2}{V_1} >0 \)
したがって、系と外界を含めた「孤立系」においても、変化が自発的に進行することがわかります。
エントロピーの定義
\( \scriptsize \color{red}{d S= \frac{\delta Q}{T}} \) 積分系で\( \scriptsize \color{red}{\Delta S= \int\frac{\delta Q}{T}} \)
熱力学第二法則 (エントロピー増大則)
断熱過程(δQ=0)において \( \scriptsize \color{red}{\Delta S \geq 0} \)
※等号 ΔS=0 … 可逆変化(準静的過程)の場合
※不等号 ΔS>0 … 自発的変化・不可逆変化(非準静的過程)の場合
非断熱の系でのエントロピー変化の考え方
系と外界をあわせた「孤立系」として考える。
非準静的過程でのΔSの求め方
始点と終点が同じ準静的過程に置き換えて熱の出入りを求め、ΔSを計算する。
