母集団と標本(サンプル)との関係は、統計のなかで重要な考え方ですが、理解しにくく混乱しやすい内容ですので、整理してまとめました。
目次
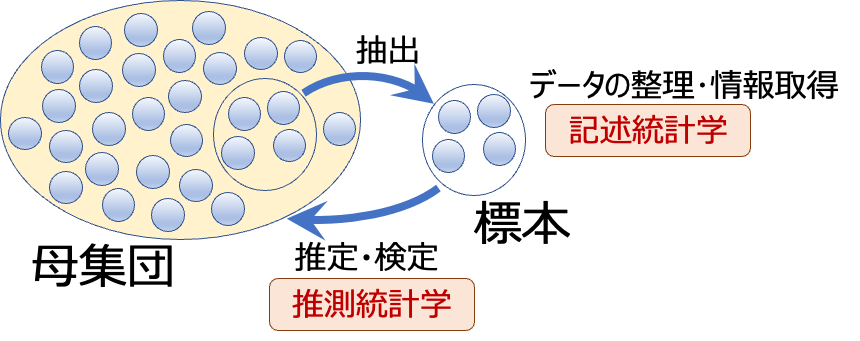
母集団は対象とする全てのデータの集合のことで、標本(サンプル)は母集団から抽出した部分的な集合のことを意味します。
たとえば、国勢調査は国民全員について調査をおこなうので母集団のデータを扱うことになります。一方、テレビの視聴率調査は一部の家庭を対象とするので標本のデータを扱っていることになります。
ところで、なぜ全部のデータを対象せずに、標本を抜き出して調べる必要があるのでしょう?
もし、母集団が小さければ全データについて調べればよいのですが、母集団が大きいケースではすべてを調査するのに多大な労力やコストがかかるために現実的には実施困難である場合があります。
また、製品の検査などの場合、非破壊で検査することができないためにそもそも全数検査が不可能な場合もあります。
そこで、部分的に抜きだした「標本」についてまとめたデータから「母集団」の性質を推測しよう、というわけです。この作業を統計的に行うのが「推測統計」です(☞統計学の分類)。
推測統計の前提として、母集団から標本を抽出する際には無作為抽出(ランダムサンプリング)である必要があります。
無作為抽出とは、標本(サンプル)を構成するデータがすべて同じ確率で抽出されることです。言い換えると、あるデータだけがほかのデータよりも選ばれやすいという状況がないことです。
ある特性をもつものだけを意図的に抽出した標本からは正しい推測ができませんよね。
ところで、この標本(サンプル)に関して、「サンプル数」「サンプルの数」と言う言葉を私たちの日常生活においても使うことがあります。
しかし、統計の分野における用語とは異なる意味で使われている場合があるので、気をつける必要があります。もしかすると「サンプル数」という言葉を “サンプリングに含まれる個体の数” の意味で使用しているかもしれませんが、統計用語としては間違っています(私も長いあいだ誤って使用していました。。。)。
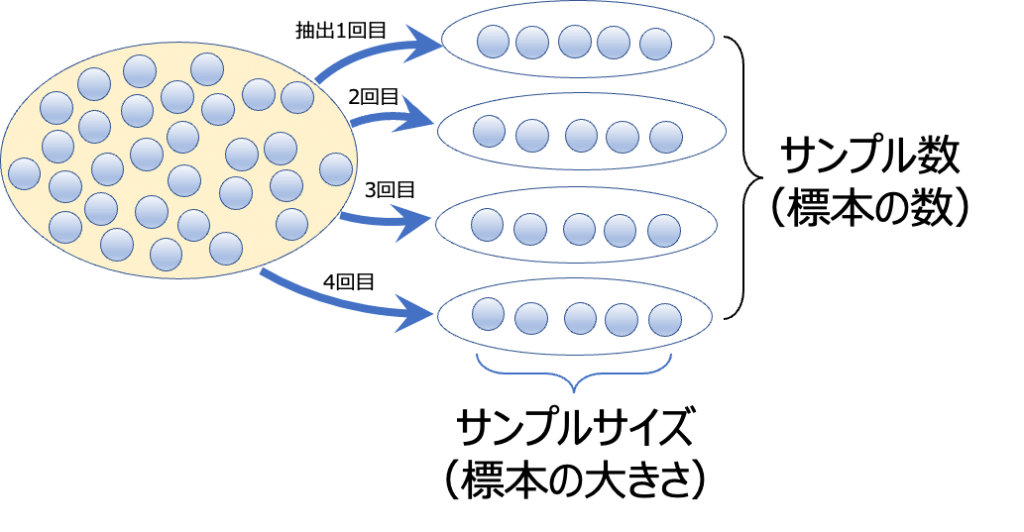
統計の用語では、一つのサンプリングに含まれる個々のデータの数のことはサンプルサイズ(標本の大きさ)といいます。
そして、サンプル数とは、抽出した標本の数、つまりサンプリングの回数を意味します。
母集団を要約する(母集団の分布を特徴づける)値のことを母数またはパラメータといいます。
母集団における平均(母平均)、分散(母平均)、標準偏差などがこれにあたります。
(確率論においては、たとえば母集団が正規分布をとることが分かっている場合、母集団の平均と分散の値が決まれば母集団の分布が決定できるので、平均と分散が母数になります。☞正規分布)
母数は、その母集団に固有の値になりますが、一般的にはその値は未知です。
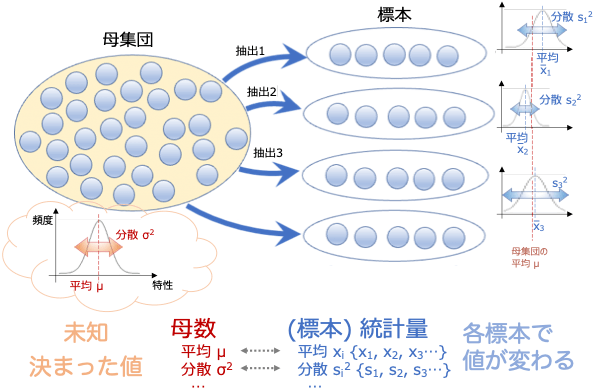
これに対して、標本を要約する値のことを統計量または標本統計量といいます。
標本における平均(標本平均)、分散(標本分散)、標準偏差などです。
統計量は、標本から得られる値であるため、サンプリングによって値が変わり、その値が確率的にきまる変数なので「確率変数」であるといえます(☞確率変数)。
これらの言葉をもちいると、「推測統計」は、母集団の母数を推測する目的で、母集団から標本を抽出して統計量を算出し、その統計量から母数を推定・検定すること、といえます。
先に述べたように、推測のなかのひとつに「推定」というものがあります。たとえば、全国の高校生からランダムに選んだ1000人の身長のデータを用いて日本の高校生の平均身長を推定する、などです。
このとき、「日本の高校生の平均身長は〇〇cmである」と一点の数値で決めてしまう推定のことを点推定といいます(一方、「日本の高校生の平均身長は〇〇cm〜△△cmの範囲に◇◇%の確率で存在する」というように、ある範囲内に存在する確率で表す推定のことを区間推定といいます。詳しくは別のタイミングでとりあげます)。
点推定をおこなうときに標本から母数を推定するための関数のことを、統計量のなかでも特に推定量といいます。標本の平均を求める式 \( \scriptsize \bar{x}= \frac{x_1+x_2+x_3+\cdots +x_n}{n} \) の \( \scriptsize \bar{x} \) がまさに推定量です。
推定量の式を使って実際に求めた数値のことを推定値といいます。
点推定の場合、推定量とそれに対応する母数(実際には未知ですが)は値が一致せず、そのあいだには誤差が生じます。
上の例で考えると、1000人をサンプリングして算出した平均身長は、全国を対象とした平均身長とは一致しません。
標本の数を増やしていくと、各標本から算出される平均身長の値は、母集団の平均身長の値を中心にばらつきをもつ分布になります。
ここでサンプルサイズを大きくしていくと、標本の平均のばらつきは減少し、値は母集団の平均に近づいていきます。このように、サンプルサイズが大きくなると推定量が母数に近づく性質のことを一致性といい、一致性をもつ推定量のことを一致推定量といいます。
後で述べる標本の平均や標本の分散は、一致性を有することから、一致推定量であるといえます。
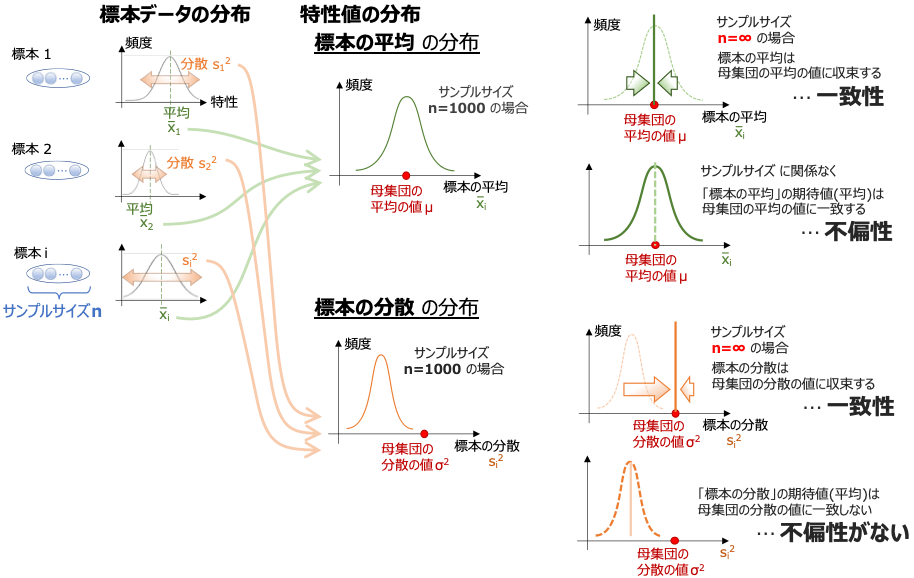
一方、サンプリングを重ねても推定値の分布が母数の値から大きく外れてしまうようでは、推定が意味をもちません。サンプルサイズによらず、推定量の期待値(平均)が母数と一致する性質のことを不偏性といい、不偏性のある推定量のことを不偏推定量といいます。
標本の平均は、先ほど述べたように一致推定量であり、かつ不偏性があるので不偏推定量でもあります。
標本の分散は、一致推定量ですが、母集団の分散に対して不偏性はないので不偏推定量にはなりません。
一致性と不偏性は推定を行ううえで重要な性質になるため、母数を推定するための推定量は、一致推定量かつ不偏推定量である必要があります。
ここで、母集団および標本の基本的な特性値(平均・分散・標準偏差)と一致性・不偏性について整理します。
母集団のデータの平均は母平均といい、\( \scriptsize \mu \) で表します。一方、抜きだした標本データの平均のことを標本平均といい、\( \scriptsize \bar{x} \) で表します。
母平均および標本平均は、下に示す式により求められます(ただし、推定統計学では、実際には母平均は直接求められません。決まった値をもつことは分かっていますが、その値は未知です)。
標本平均は、母平均の一致推定量かつ不偏推定量であることがわかっているので、点推定の場合、標本平均はそのまま母平均の推定値として使われます。
母平均 \(\scriptsize \mu=\normalsize\frac{1}{N} \scriptsize\sum x_i \) \( \tiny N \): 母集団のサイズ
標本平均 \(\scriptsize \bar{x}=\normalsize\frac{1}{n} \scriptsize\sum x_i \) \( \tiny n \): サンプルのサイズ
母集団のデータの分散は母分散といい、\(\scriptsize{\sigma^2}\) で表します。一方、標本データの分散のことを標本分散といい、\(\scriptsize{s^2}\) で表します。
分散は平均の場合とは異なって、標本分散の期待値は母分散に一致しません(母分散より小さい)。つまり、標本分散の値はそのまま母分散の推定値としては使えません。そこで、母分散を点推定するための不偏推定量として不偏分散 \(\scriptsize{u^2}\) をもちいます(\(\scriptsize{n}\) の代わりに \(\scriptsize{n-1}\) で割ります。)。
母分散 \( \scriptsize \sigma^{2}= \normalsize \frac{1}{N} \scriptsize\sum \left(x_i-\mu \right)^{2}\) \( \tiny N\): 母集団のサイズ \( \tiny \mu\): 母平均
標本分散 \( \scriptsize s^2= \normalsize \frac{1}{n} \scriptsize\sum \left(x_i-\bar x \right)^{2}\) (…推定には使えない)
不偏分散 \( \scriptsize u^2= \normalsize \frac{1}{n-1} \scriptsize\sum \left(x_i-\bar x \right)^{2}\) \( \tiny n\): サンプルのサイズ \( \tiny \bar{x}\): 標本平均
※注意 標本分散と不偏分散を区別せずに、不偏推定量として \( \tiny s^2= \scriptsize \frac{1}{n-1} \tiny \sum \left(x_i-\bar x \right)^{2}\) とする教科書、資料などもあります(実際、自分も区別せずに教わり、そのように使っていました)。
Excel関数:
母分散 var.p(x1, x2, …) または varp(x1, x2, …)
不偏分散 var.s(x1, x2, …) または var(x1, x2, …)
母集団の標準偏差は \(\scriptsize{\sigma}\) (シグマと呼ぶ)、サンプルの標準偏差は 標本標準偏差 \(\scriptsize{s}\) と表します。
標準偏差は分散の場合と同様、標本標準偏差の期待値が母集団の標準偏差に一致しません(分散の平方根なので、当たり前といえばその通りなのですが)。そこで、不偏推定量として不偏標準偏差 \( \scriptsize u \) をもちいて母集団の点推定をおこないます。
母集団の標準偏差 \( \scriptsize \sigma=\sqrt{\sigma^{2}}=\sqrt{\frac{1}{N} \tiny \sum \left(x_i-\mu \right)^{2}}\)
標本標準偏差 \( \scriptsize s=\sqrt{s^{2}}=\sqrt{ \frac{1}{n} \tiny \sum \left(x_i-\bar x \right)^{2}}\) (…推定には使えない)
不偏標準偏差 \( \scriptsize u=\sqrt{u^{2}}=\sqrt{ \frac{1}{n-1} \tiny \sum \left(x_i-\bar x \right)^{2}}\)
※注意 標本標準偏差と不偏標準偏差を区別せずに、不偏推定量として \( \tiny s=\sqrt{ \scriptsize \frac{1}{n-1} \tiny \sum \left(x_i-\bar x \right)^{2}}\) とする教科書、資料などもあります。
Excel関数:
母集団の標準偏差 stdev.p(x1, x2, …) または stdevp(x1, x2, …)
不偏標準偏差 stdev.s(x1, x2, …) または stdev(x1, x2, …)
